DISTRIBUCIONES MUESTRALES

                                4.2 DISTRIBUCIÓN BINOMIAL

De acuerdo a (Levin, richard I. y Rubin, David S., 2010)

“Una distribución de probabilidad de variable aleatoria discreta utilizada ampliamente es la distribución binomial. Esta distribución describe una variedad de procesos de interés para los administradores. Por otra parte, describe datos discretos, no continuos, que son resultado de un experimento conocido como proceso de Bernoulli, en honor del matemático suizo nacido en el siglo XVII, Jacob

Bernoulli.” (Pág. 191)

Según (Murray R. Spiegel, 1991)

“Si p es la probabilidad de que ocurra un suceso en un solo intento (llamada probabilidad de éxito) y q = 1 – p es la probabilidad de que no ocurra en un solo intento (llamada probabilidad de fracaso), entonces la probabilidad de que el suceso ocurra exactamente X veces en N intentos (o sea, X éxitos y N – X fracasos) viene dada por: “(Pág. 159)

De acuerdo a (Humberto Gutiérrez Pulido y Román de la Vara Salazar, 2009)

“Proporciona la probabilidad de observar x éxitos en una secuencia de n experimentos Bernoulli independientes con una probabilidad constante p de éxito. Entonces este experimento recibe el nombre de experimento binomial. La variable aleatoria X, que es igual al número de ensayos donde el resultado es un éxito, tiene una distribución binomial (n, p). La función de probabilidades de X es,

Ejemplo;

Levin, richard I. y Rubin, David S., 2010, señala que:

“Las posibilidades de obtener exactamente dos caras (en cualquier orden) en tres lanzamientos de una moneda no alterada. Simbólicamente, expresamos los valores de la forma siguiente:

• p _ probabilidad característica o probabilidad de tener éxito _ 0.5

• q _ 1 _ p _ probabilidad de fracaso _ 0.5

• r _ número de éxitos deseados _ 2

• n _ número de intentos hechos _ 3

Probabilidad de 2 éxitos en 3 intentos = (3! / 2! (3- 2)!) (0.5)^2 (0.5)^1

                                                             = (3*2*1 / (2*1)(1*1)) (0.5)^2(0.5)

                                                             = (6/2)(0.25)(0.5)

                                                             = 0.375

Por tanto, existe una probabilidad de 0.375 (37.5%) de obtener dos caras en tres lanzamientos de una moneda no alterada.” (Pág. 192)

Murray R. Spiegel, 1991, señala que:

“La probabilidad de obtener exactamente 2 caras en 6 tiradas de una moneda es:

(Dennis D. Wackerly, William Mendenhall y Richard L. Scheaffer, 2010, señalan que:

“Suponga que un lote de 5000 fusibles eléctricos contiene 5% de piezas defectuosas. Si se prueba una muestra de 5 fusibles, encuentre la probabilidad de hallar al menos uno defectuoso.

Solución Es razonable suponer que Y, el número observado de defectuosos, tiene una distribución binomial aproximada porque el lote es grande. Retirar unos cuantos fusibles no cambia lo suficiente la composición de los restantes como para preocuparnos. Entonces,

Observe que hay una probabilidad más bien grande de ver al menos uno defectuoso, aun cuando la muestra sea muy pequeña.” (Pág. 105)

4.3 DISTRIBUCIÓN HIPERGEOMÉTRICA.

De acuerdo a  (Humberto Gutiérrez Pulido y Román de la Vara Salazar, 2009)

“Da la probabilidad de obtener X éxitos en n experimentos Bernoulli, donde la probabilidad de éxito cambia de un experimento al siguiente. Sea X el número de éxitos en la muestra, entonces X tiene una distribución hipergeométrica.” (Pág.50)

Segùn (Dennis D. Wackerly, William Mendenhall y Richard L. Scheaffer, 2010)

“Se dice que una variable aleatoria Y  tiene una distribución de probabilidad hipergeométrica si y sólo si

donde y es un entero 0, 1, 2,…, n, sujeto a las restricciones y ≤ r y n – y ≤ N – r.” (Pág. 126)

De acuerdo a (Jay L. Devore, 2008)

“Si X es el número de éxitos (E) en una muestra completamente aleatoria de tamaño n extraída de la población compuesta de M éxitos y (N _ M) fallas, entonces la distribución de probabilidad de X llamada distribución hipergeométrica, es

con x un entero que satisface máx(0, n _ N _ M) _ x _ mín(n, M).” (Pág. 117)

Ejemplo

Dennis D. Wackerly, William Mendenhall y Richard L. Scheaffer, 2010, señalan que:

“Un problema importante encontrado por directores de personal y otros que se enfrentan a la selección del mejor candidato en un conjunto fi nito de elementos, queda ejemplificado en la siguiente situación. De un grupo de 20 ingenieros con título de Ph.D, 10 de ellos son seleccionados al azar para un empleo. ¿Cuál es la probabilidad de que los 10 seleccionados incluyan los cinco mejores ingenieros del grupo de 20?

Solución Para este ejemplo, N = 20, n = 10 y r = 5. Esto es, hay sólo 5 en el conjunto de 5 mejores ingenieros y buscamos la probabilidad de que Y = 5, donde Y denota el número de mejores ingenieros entre los diez seleccionados. Entonces

Segùn (Jay L. Devore, 2008)

“Se capturaron, etiquetaron y liberaron cinco individuos de una población de animales que se piensa están al borde de la extinción en una región para que se mezclen con la población. Después de haber tenido la oportunidad de mezclarse, se selecciona una muestra aleatoria de 10 de estos animales. Sea X = el número de animales etiquetados en la segunda muestra. Si en realidad hay 25 animales de este tipo en la región, ¿cuál es la probabilidad de que a) X = 2? b) ¿X ≤ 2?

Los valores de los parámetros son n = 10, M = 5 (cinco animales etiquetados en la población) y N = 25, por lo tanto

Para el inciso a)

Para el inciso b)

4.4 DISTRIBUCIÓN DE POISSON.

De acuerdo a (Humberto Gutiérrez Pulido y Román de la Vara Salazar, 2009)

“Una situación frecuente en control de calidad es evaluar variables como las siguientes: número de defectos por artículo, número de impurezas en un líquido, número de errores de un trabajador. Todos los casos anteriores se resumen así: número de eventos que ocurren por unidad (por unidad de área, por unidad de volumen, por unidad de tiempo, etc.). Asimismo, es frecuente que este tipo de variables tenga una distribución de Poisson, cuya función de distribución de probabilidades está dada por:

Según  (Levin, richard I. y Rubin, David S., 2010)

“La distribución de Poisson se utiliza para describir ciertos tipos de procesos, entre los que se encuentran la distribución de llamadas telefónicas que llegan a un conmutador, las llegadas de camiones y automóviles a una caseta de cobro, y el número de accidentes registrados en cierta intersección. Estos ejemplos tienen en común un elemento: pueden ser descritos mediante una variable aleatoria discreta que toma valores enteros (0, 1, 2, 3, 4, 5, etc). La probabilidad de tener exactamente x ocurrencias en una distribución de Poisson se calcula con la fórmula:” (Pág. 202)

De acuerdo a (Dennis D. Wackerly, William Mendenhall y Richard L. Scheaffer, 2010)

“Se dice que una variable aleatoria Y tiene distribución de probabilidad de Poisson si y solo si:

Ejemplo;

Humberto Gutiérrez Pulido y Román de la Vara Salazar, 2009, señalan que:

“En una empresa se reciben en promedio 5 quejas diarias por mal servicio.

Si el número de quejas por día se distribuye Poisson con λ = 5, ¿cuál es la probabilidad de no recibir quejas en un día? Esto se obtiene con:

Esta probabilidad de 0.007 es muy baja, por lo que en realidad sería muy raro que en un día no se recibiera ninguna queja.” (Pág. 51)

Levin, richard I. y Rubin, David S., 2010, señalan que:

“El número de accidentes está distribuido de acuerdo con una distribución de Poisson, y el Departamento de Seguridad de Tránsito desea que calculemos la probabilidad de que en cualquier mes ocurran exactamente 2 accidentes. Aplicando la fórmula.” (Pág. 203)

De acuerdo a (Dennis D. Wackerly, William Mendenhall y Richard L. Scheaffer, 2010)

“Suponga que se diseña un sistema aleatorio de patrulla de policía para que un oficial de patrulla pueda estar en un lugar de su ruta Y = 0, 1, 2, 3,. . . veces por periodo de media hora, con cada lugar visitado un promedio de una vez por periodo.

Suponga que Y posee, aproximadamente, una distribución de probabilidad de Poisson. Calcule la probabilidad de que el oficial de patrulla no llegue a un lugar determinado durante un periodo de media hora. ¿Cuál es la probabilidad de que el lugar sea visitado una vez?

Solución: Para este ejemplo el periodo es media hora y el número medio de visitas por intervalo de media hora es l = 1. Entonces

El evento de que un lugar determinado no sea visitado en un periodo de media hora corresponde a (Y = 0), y

Del mismo modo,

La probabilidad de que el lugar sea visitado al menos una vez es el evento (Y ≥ 1). Entonces

4.5 ESPERANZA MATEMÁTICA.

De acuerdo a n(Murray R. Spiegel, 1991)

“Si p es la probabilidad de que una persona reciba una cantidad S de dinero, la esperanza matemática (o simplemente esperanza) se define como pS. Si X denota una variable aleatoria discreta que puede tomar los valores X1, X2,…, Xk con probabilidades P1, P2,…, Pk, donde P1 + P2 +… + Pk = 1, La esperanza matemática de X, denotada E(X), y se define como:” (Pág.133)

Ejemplo

Murray R. Spiegel, 1991, señala que:

“Si la probabilidad de que un hombre gane un premio de $10 es 1/5, su esperanza matemática es 1/5($10) = 2.” (Pág. 133)

4.6 DISTRIBUCIÓN NORMAL.

Según (Humberto Gutiérrez Pulido y Román de la Vara Salazar, 2009)

“La distribución normal es una distribución continua cuya densidad tiene forma de campana. Si X es una variable aleatoria normal, entonces su función de densidad de probabilidades está dada por:

donde μ es su media, y σ su desviación estándar. Al graficar la función f (x) se obtiene una gráfica simétrica y unimodal, cuya forma es similar a una campana. El centro de ésta coincide con μ, y la amplitud está determinada por σ.” (Pág. 51)

De acuerdo a (Dennis D. Wackerly, William Mendenhall y Richard L. Scheaffer, 2010)

 “Se dice que una variable Y tiene una distribución normal de probabilidad si y solo si, para σ > 0 y –∞< μ < ∞, la función de densidad de Y es: “(Pág. 178)

Según (Jay L. Devore, 2008)

“Se dice que una variable aleatoria continua X tiene una distribución normal con parámetros μ y σ (0 μ y σ²), donde –∞< μ < ∞ y σ > 0 , si la función de densidad de probabilidad de X es: “ (Pág. 145)

De acuerdo a (Murray R. Spiegel y Larry J. Stephens, 2009)

“Uno de los ejemplos más importantes de distribución de probabilidad continua es la distribución normal, curva normal o distribución gaussiana, que se define mediante la ecuación

donde μ = media, σ = desviación estándar, π = 3.14159 … y e = 2.71828 ..., el total del área, que está limitada por la curva y por el eje X es 1; por lo tanto, el área bajo la curva comprendida entre X = a y X = b, donde a < b representa la probabilidad de que X se encuentre entre a y b. Esta probabilidad se denota por Pr{a < X < b}.” (Pág. 173)

Ejemplo

Dennis D. Wackerly, William Mendenhall y Richard L. Scheaffer, 2010, señalan que:

“Las calificaciones para un examen de admisión a una universidad están normalmente distribuidas con media de 75 y desviación estándar 10...Que fracción de las calificaciones se encuentra entre 80 y 90?

Solución: Recuerde que z es la distancia desde la media de una distribución normal expresada en unidades de desviación estándar. Entonces,

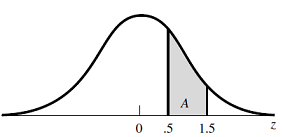
Entonces la fracción deseada de la población está dada por el área entre

Esta área esta sombreada en la figura, usted puede ver que A = A(.5) – A(1.5) = .3085 – .0668 = .2417.” (Pág. 180 y 181)

4.7 DISTRIBUCIÓN T-STUDENT.

De acuerdo a (Murray R. Spiegel y Larry J. Stephens, 2009)

“Si se consideran muestras de tamaño N extraídas de una población normal (o aproximadamente normal) cuya media es μ y si para cada muestra se calcula t, usando la media muestral X’ y la desviación estándar muestral s o s^, se obtiene la distribución muestral de t. Esta distribución está dada por: “(Pág. 275)

Según  (Humberto Gutiérrez Pulido y Román de la Vara Salazar, 2009)

“Sea Z una variable aleatoria con distribución normal estándar y sea V una variable aleatoria con distribución ji-cuadrada con k grados de libertad. Si Z y V son independientes, entonces la variable aleatoria,

tiene una distribución T con k grados de libertad, cuya función de densidad de probabilidad está dada por:

La media y la varianza de esta distribución están dadas por, E(X) = 0 y σ 2 = k/(k − 2) para k > 2. Una de las principales aplicaciones de la distribución T de Student es fundamentar las inferencias sobre la media μ de una población. Debido a que si se obtiene una muestra aleatoria de tamaño n de una población cuya distribución es normal, entonces el estadístico:

sigue una distribución T de Student con n – 1 grados de libertad. En la tabla A4 del apéndice se dan valores para los diferentes cuantiles o puntos críticos de esta distribución.

(William Mendenhall, Robert J. Beaver y Barbara M. Beaver, 2010) exponen que:

“para muestras aleatorias de tamaño n desde una población normal y publicó sus resultados bajo el nombre de “Student”. Desde entonces, la estadística se conoce como t de Student. Tiene las siguientes características:

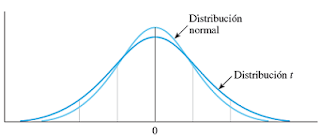
Tiene forma de montículo y es simétrica alrededor de t _ 0, igual que z.

• Es más variable que z, con “colas más pesadas”; esto es, la curva t no aproxima al eje horizontal con la misma rapidez que z. Esto es porque el estadístico t abarca dos cantidades aleatorias, x_ y s, en tanto que el estadístico z tiene sólo la media muestral, x_. Se puede ver este fenómeno en la fi gura 10.1.

• La forma de la distribución t depende del tamaño muestral n. A medida que n aumenta, la variabilidad de t disminuye porque la estimación s de s está basada en más y más información. En última instancia, cuando n sea infinitamente grande, las distribuciones t y z son idénticas.” (Pág. 388)

Ejemplo

De acuerdo a (Ronald E. Walpole, Raymond H. Myers, Sharon l. Myers y Keying Ye, 2012)

 “Un ingeniero químico afirma que el rendimiento medio de la población de un cierto proceso de lotes es 500 gramos por mililitro de materia prima. Para verificar dicha afirmación muestrea 25 lotes cada mes. Si el valor t calculado cae entre – t 0.05 y t0.05, queda satisfecho con su afirmación. ¿Qué conclusión debería sacar de una muestra que tiene una media ￣x = 518 gramos por mililitro y una desviación estándar muestral s = 40 gramos?

Suponga que la distribución de rendimientos es aproximadamente normal.

Solución: En la tabla A.4 encontramos que t 0.05 = 1.711 para 24 grados de libertad. Por lo tanto, el ingeniero quedara satisfecho con esta afirmación si una muestra de 25 lotes rinde un valor t entre –1.711 y 1.711. Si μ = 500, entonces,

un valor muy superior a 1.711. La probabilidad de obtener un valor t, con v = 24, igual o mayor que 2.25, es aproximadamente 0.02. Si μ > 500, el valor de t calculado de la muestra seria más razonable. Por lo tanto, es probable que el ingeniero concluya que el proceso produce un mejor producto del que pensaba.” (Pág. 250)

4.8 DISTRIBUCIÓN CHI CUADRADA.

Según (Ronald E. Walpole, Raymond H. Myers, Sharon l. Myers y Keying Ye, 2012)

“La variable aleatoria continua X tiene una distribución chi cuadrada, con v grados de libertad, si su función de densidad es dada por

donde v es un entero positivo.”(Pág. 200)

De acuerdo a (Douglas C. Montgomery y George C.Runger, 2001)

“La distribución chi cuadrada es una de las distribuciones de muestreo con mayor utilidad. Está definida en términos de variables aleatorias normales.

Sean Z1, Z2, …, Zk variables aleatorias distribuidas normal e independientemente, con media μ = 0 y varianza σ² = 1. Entonces, la variable aleatoria

 

Tiene la función de densidad de probabilidad

Y se dice que sigue una distribución chi cuadrada con K grados de libertad lo que se abrevia como X.” (Pág. 309)

Según  (Humberto Gutiérrez Pulido y Román de la Vara Salazar, 2009)

“Sean Z1, Z2, ..., Zk variables aleatorias independientes, con distribución normal estándar (μ = 0 y σ 2 = 1), entonces la variable aleatoria

sigue una distribución ji-cuadrada con k grados de libertad, y su función de densidad de probabilidad está dada por:

donde Γ (⋅) es la función gama que está definida por: “(Pág. 57)

(Murray R. Spiegel y Larry J. Stephens, 2009) menciona que:

“Sea el estadístico

donde χ es la letra griega ji y χ2 se lee “ji cuadrada”. Si se consideran muestras de tamaño N obtenidas de una población normal cuya desviación estándar es σ, y si para cada muestra se calcula χ2, se obtiene una distribución muestral de χ2. Esta distribución, llamada distribución ji cuadrada, está dada por

donde ν = N − 1 es el número de grados de libertad y Y0 es una constante que depende de ν, de manera que el área bajo la curva sea 1.” (Pág. 277-278)

Ejemplo

Murray R. Spiegel y Larry J. Stephens, 2009, señalan que:

“La desviación estándar en los pesos de paquetes de 40.0 onzas (oz), llenados con una máquina, ha sido 0.25 oz. En una muestra de 20 paquetes se observa una desviación estándar de 0.32 oz. ¿Este aparente incremento en la variabilidad es significativo a los niveles: a) 0.05 y b) 0.01?

SOLUCIÓN

Decidir entre las hipótesis:

H0 : σ = 0.25 oz, el resultado observado es casualidad.

H1 : σ > 0.25 oz, la variabilidad ha aumentado.

El valor de χ2 para la muestra es

a) Empleando una prueba de una cola, al nivel de significancia 0.05, se rechaza H₀ si los valores muestrales de χ2 son mayores a X².₉₅, lo que es igual a 30.1 para ν = 20 − 1 = 19 grados de libertad. Por lo tanto, se rechaza H₀ al nivel de significancia 0.05.

b) Empleando una prueba de una cola, al nivel de significancia 0.01, se puede rechazar H₀ si los valores muestrales de χ2 son mayores a X².₉₉, lo que es igual a 36.2 para 19 grados de libertad. Por lo tanto, al nivel de significancia 0.01, no se rechaza H₀.

Se concluye que la variabilidad probablemente ha aumentado. Se recomienda examinar la máquina.” (Pág. 289)

4.9 DISTRIBUCIÓN F.

De acuerdo a (Ronald E. Walpole, Raymond H. Myers, Sharon l. Myers y Keying Ye, 2012)

“Sean U y V dos variables aleatorias independientes que tienen distribuciones chi cuadrada con v1 y v2 grados de libertad, respectivamente. Entonces, la distribución de la variable aleatoria  es dada por la función de densidad

Esta se conoce como la distribución F con v1 y v2 grados de libertad” (Pág. 251)

Según (William G. Marchal y Samuel A. Wathen, 2008)

“La distribución F, la cual debe su nombre a sir Ronald Fisher, uno de los pioneros de la estadística actual. Esta distribución de probabilidad sirve como la distribución del estadístico de prueba para varias situaciones. Con ella se pone a prueba si dos muestras provienen de poblaciones que tienen varianzas iguales, y también se aplica cuando se desean comparar varias medias poblacionales en forma simultánea. La comparación simultánea de varias medias poblacionales se denomina análisis de la varianza (ANOVA). En las dos situaciones, las poblaciones deben seguir una distribución normal, y los datos deben ser al menos de escala de intervalos.” (Pág. 407)

Según  (Humberto Gutiérrez Pulido y Román de la Vara Salazar, 2009)

“Sean W y Y variables aleatorias ji-cuadrada independientes con u y v grados de libertad, respectivamente. Entonces el cociente,

tiene una distribución F con u grados de libertad en el numerador, y v en el denominador, cuya función de densidad de probabilidad está dada por: “(Pág. 59)

De acuerdo a (Murray R. Spiegel y Larry J. Stephens, 2009)

“La distribución muestral de F se le llama distribución F de Fisher, o simplemente distribución F, con ν1 = N1− 1 y ν2 = N2 − 1 grados de libertad. Esta distribución está dada por

donde C es una constante que depende de ν1 y ν2, de manera que el área total bajo la curva sea 1, aunque esta forma puede variar de manera notable de acuerdo con los valores de ν1 y ν2.” (Pág. 279)

LISTA DE REFERENCIAS BIBLIOGRAFICAS

Levin, richard I. y Rubin, David S., 2010, Estadística para administración y economía, Séptima edición, México, PEARSON EDUCACIÓN.

Murray R. Spiegel, 1991, Estadística, segunda edición, Chile, McGraw-Hill.

Humberto Gutiérrez Pulido y Román de la Vara Salazar, 2009, Control estadístico de calidad y seis sigma, segunda edición, México, McGraw-Hill.

Dennis D. Wackerly, William Mendenhall y Richard L. Scheaffer, 2010, Estadística matemática con aplicaciones, séptima edición, México,  Cengage Learning Editores.

Jay L. Devore, 2008, Probabilidad y estadística para ingeniería y ciencias, séptima edición, México, Cengage Learning Editores.

Ronald E. Walpole, Raymond H. Myers, Sharon l. Myers y Keying Ye, 2012, Probabilidad y estadística para ingeniería y ciencias, Novena edición, México, Pearson educación.

William G. Marchal y Samuel A. Wathen, 2008, Estadística aplicada a los negocios y la economía, México, McGraw-Hill.

Murray R. Spiegel y Larry J. Stephens, 2009, Estadística, cuarta edición, México, McGraw-Hill.

William Mendenhall, Robert J. Beaver y Barbara M. Beaver, 2010, Introducción a la probabilidad y estadística, Décima tercera edición, México, Cengage Learning Editores.